
In Chapter 41, Kepler returned to analyzing the shape of the orbit of Mars. He had first discussed the idea of an oval motion for the planet back in Chapter 30, and returns to the method of proof (or disproof) by reductio ad absurdum, as described in Chapter 16:
“It is not unusual, whether in geometry, or arithmetic, or dialectic, to use a form of argument which leads to an absurdity, so that if something absurd is seen to follow from the assumptions, they are rejected as false; and this is carried out until the consequent removal of excesses and defects unveils the exact truth (which in the mathematical disciplines is a mean between the two).” (Donahue translation, p. 254)
Kepler set out to discover if the assumption that Mars' orbit is a circle contradicts results he had arrived at earlier.
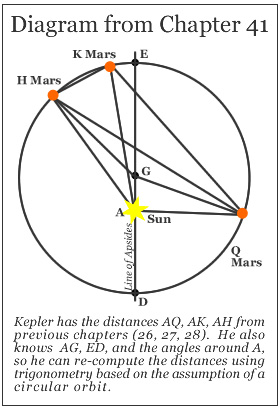
To do this, he compared the Sun-Mars distance measures that he computed previously in Chapters 26, 27, and 28 with the distances a perfect-circle model of the orbit would require for observations corresponding to these lines of sight from Mars to the Sun.
He had Sun-Mars distance measures for AH, AK, and AQ in the diagram as a result of his earlier work.
He then used various postulates of geometry to compute what these distances would be, based upon the assumption that the orbit described a perfect circle. Kepler knew the length AG (the “eccentricity” of the Mars’ orbit) from his test that disproved “Vicarious Hypothesis.”
He also knew the orientation of the line ED with respect to the Zodiac.
| AK | AH | AQ | |
|---|---|---|---|
| The distances computed using the circular geometric construction were: | 166,605 | 163,883 | 148,539 |
| However, based upon his research noted in Chapters 26,27, and 28, Kepler had computed these distances as: | 166,225 | 163,100 | 147,750 |
| Difference | 380 | 783 | 789 |
Kepler’s working notes show that he thought he must have made an error when he first made this comparison. Not until late in his process of discovery did he abandon the idea of a circular orbit for Mars.
"And me, Christ! - I had triumphed [over Mars] for two full years" he exclaimed upon the revelation. (Donahue translation, p. 451)
"My first error," he related, "was to suppose that the path of the planet is a perfect circle, a supposition that was all the more noxious a thief of time the more it was endowed with the authority of all philosophers, and the more convenient it was for metaphysics in particular.” (Donahue translation, p. 417)
The animation below shows how two sets of measures for distance could determine different circles but correspond to the same oval shape.
In Chapter 44, Kepler wrote: “Clearly, then, [what is to be said] is this: the orbit of the planet is not a circle, but comes in gradually on both sides and returns again to the circle’s distance at perigee. They are accustomed to call the shape of this sort of path an oval.” (Donahue translation, p. 543. "Perigee" is the point on the orbit in a heliocentric model where the planet is nearest to the Sun.)
Kepler then investigated what geometrical constructions could produce an oval motion, returning to the Copernican and Ptolemaic modes of thought as he sought a mathematical mechanism to produce the new orbital shape.
Yet, each device he constructed failed on the grounds of either accuracy of metaphysical implausibility. In Chapter 51, he sets aside his hypotheses in Chapters 45 through 50.



